Tyler James Burch

Applying research methods, statistics, machine learning, and Bayesian modeling to solve problems in professional baseball analytics.

2024 Rewind: Polynomial Regression in Bambi

Back in 2024, I wrote a couple of example notebooks that got merged into the Bambi documentation. For those unfamiliar, Bambi is a library for fitting Bayesian regression models using a formulaic interface on top of PyMC (the closest thing in python to brms, in my opinion). I realized I never migrated the content here, so I thought it was time to do so.

This first post covers polynomial regression. I’ll update next week with a companion post digging deeper into orthogonal polynomials. The original notebook lives in the Bambi docs.

What follows is the content from the notebook, lightly adapted for this blog format.

Polynomial Regression

Unlike many other examples shown in Bambi, there aren’t specific polynomial methods or families implemented – most of the interesting behavior for polynomial regression occurs within the formula definition. Regardless, there are some nuances that are useful to be aware of.

This example uses the kinematic equations from classical mechanics as a backdrop. Specifically, an object in motion experiencing constant acceleration can be described by the following:

\[x_f = \frac{1}{2} a t^2 + v_0 t + x_0\]

where \(x_0\) and \(x_f\) are the initial and final locations, \(v_0\) is the initial velocity, and \(a\) is acceleration.

A falling ball

First, we’ll consider a simple falling ball, released from 50 meters. In this situation, \(v_0 = 0\) \(m\)/\(s\), \(x_0 = 50\) \(m\) and \(a = g\), the acceleration due to gravity, \(-9.81\) \(m\)/\(s^2\). So dropping out the \(v_0 t\) component, the equation takes the form:

\[x_f = \frac{1}{2} g t^2 + x_0\]

We’ll start by simulating data for the first 2 seconds of motion. We will also assume some measurement error with a gaussian distribution of \(\sigma = 0.3\).

import warnings

import arviz as az
import bambi as bmb
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

SEED = 1234
az.style.use("arviz-darkgrid")
warnings.filterwarnings("ignore")

g = -9.81  # acceleration due to gravity (m/s^2)
t = np.linspace(0, 2, 100)  # time in seconds
inital_height = 50
x_falling = 0.5 * g * t**2 + inital_height

rng = np.random.default_rng(SEED)
noise = rng.normal(0, 0.3, x_falling.shape)
x_obs_falling = x_falling + noise
df_falling = pd.DataFrame({"t": t, "x": x_obs_falling})

fig, ax = plt.subplots(figsize=(10, 6))
ax.scatter(t, x_obs_falling, label="Observed Displacement", color="C0")
ax.plot(t, x_falling, label="True Function", color="C1")
ax.set(xlabel="Time (s)", ylabel="Displacement (m)")
ax.legend();

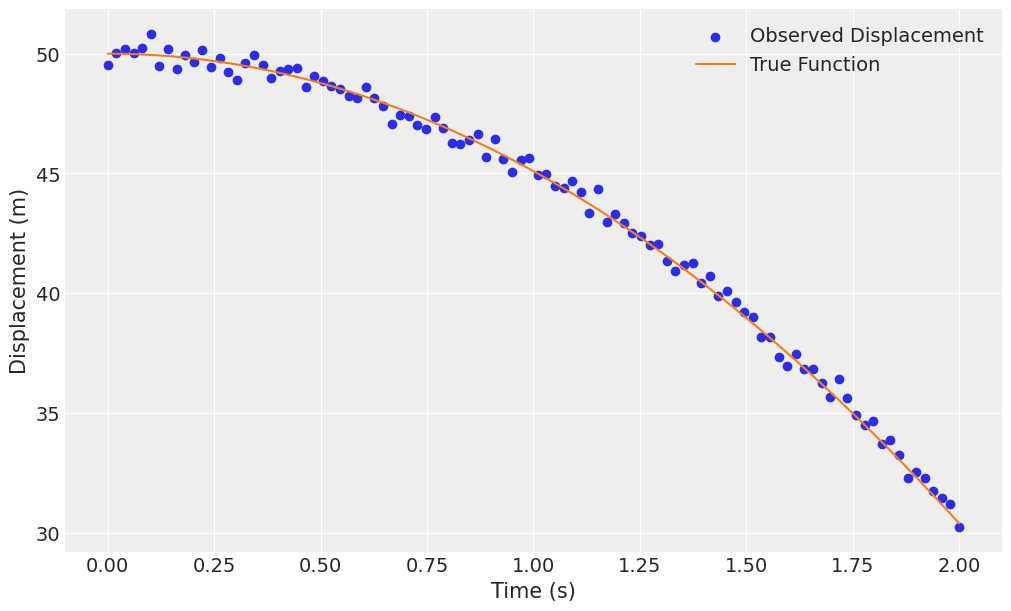
Falling ball data

Casting the equation \(x_f = \frac{1}{2} g t^2 + x_0\) into a regression context, fitting:

\[x_f = \beta_0 + \beta_1 t^2\]

We let time (\(t\)) be the independent variable, and final location (\(x_f\)) be the response/dependent variable. This allows our coefficients to be proportional to \(g\) and \(x_0\). The intercept, \(\beta_0\) corresponds exactly to \(x_0\), the initial height. Letting \(\beta_1 = \frac{1}{2} g\) gives \(g = 2\beta_1\) when \(x_1 = t^2\), meaning we’re doing polynomial regression. We can put this into Bambi via the following, optionally including the + 1 to emphasize that we choose to include the coefficient.

model_falling = bmb.Model("x ~ I(t**2) + 1", df_falling)
results_falling = model_falling.fit(idata_kwargs={"log_likelihood": True}, random_seed=SEED)

The term I(t**2) indicates to evaluate inside the I. For including just the \(t^2\) term, you can express it in any of the following ways:

I(t**2)
{t**2}
Square the data directly, and pass it as a new column

To verify, we’ll fit the other two versions as well.

model_falling_variation1 = bmb.Model(
    "x ~ {t**2} + 1",  # Using {t**2} syntax
    df_falling
)
results_variation1 = model_falling_variation1.fit(random_seed=SEED)

model_falling_variation2 = bmb.Model(
    "x ~ tsquared + 1",  # Using data with the t variable squared
    df_falling.assign(tsquared=t**2)
)
results_variation2 = model_falling_variation2.fit(random_seed=SEED)

print("I{t**2} coefficient: ", round(results_falling.posterior["I(t ** 2)"].values.mean(), 4))
print("{t**2} coefficient: ", round(results_variation1.posterior["I(t ** 2)"].values.mean(), 4))
print("tsquared coefficient: ", round(results_variation2.posterior["tsquared"].values.mean(), 4))

I{t**2} coefficient:  -4.8476
{t**2} coefficient:  -4.8476
tsquared coefficient:  -4.8476

Each of these provides identical results, giving -4.9, which is \(g/2\). This makes the acceleration exactly the \(-9.81\) \(m\)/\(s^2\) acceleration that generated the data. Looking at our model summary,

az.summary(results_falling)

             mean     sd  hdi_3%  hdi_97%  mcse_mean  mcse_sd  ess_bulk  ess_tail  r_hat
sigma       0.336  0.025   0.289    0.381      0.000    0.000    5977.0    2861.0    1.0
Intercept  49.961  0.051  49.870   50.058      0.001    0.001    5997.0    3145.0    1.0
I(t ** 2)  -4.848  0.028  -4.899   -4.799      0.000    0.000    5704.0    2844.0    1.0

We see that both \(g/2 = -4.9\) (so \(g=-9.81\)) and the original height of \(x_0 = 50\) \(m\) are recovered, along with the injected noise.

We can then use the model to answer some questions, for example, when would the ball land? This would correspond to \(x_f = 0\).

\[0 = \frac{1}{2} g t^2 - x_0\] \[t = \sqrt{2x_0 / g}\]

calculated_x0 = results_falling.posterior["Intercept"].values.mean()
calculated_g = -2 * results_falling.posterior["I(t ** 2)"].values.mean()
calculated_land = np.sqrt(2 * calculated_x0 / calculated_g)
print(f"The ball will land at {round(calculated_land, 2)} seconds")

The ball will land at 3.21 seconds

Or if we want to account for our measurement error and use the full posterior,

calculated_x0_posterior = results_falling.posterior["Intercept"].values
calculated_g_posterior = -2 * results_falling.posterior["I(t ** 2)"].values
calculated_land_posterior = np.sqrt(2 * calculated_x0_posterior / calculated_g_posterior)
lower_est = round(np.quantile(calculated_land_posterior, 0.025), 2)
upper_est = round(np.quantile(calculated_land_posterior, 0.975), 2)
print(f"The ball landing will be measured between {lower_est} and {upper_est} seconds")

The ball landing will be measured between 3.2 and 3.23 seconds

Projectile Motion

Next, instead of a ball strictly falling, instead imagine one thrown straight upward. In this case, we add the initial velocity back into the equation.

\[x_f = \frac{1}{2} g t^2 + v_0 t + x_0\]

We will envision the ball tossed upward, starting at 1.5 meters above ground level. It will be tossed at 7 m/s upward. It will also stop when hitting the ground.

v0 = 7
x0 = 1.5
x_projectile = (1/2) * g * t**2 + v0 * t + x0
noise = rng.normal(0, 0.2, x_projectile.shape)
x_obs_projectile = x_projectile + noise
df_projectile = pd.DataFrame({"t": t, "tsq": t**2, "x": x_obs_projectile, "x_true": x_projectile})
df_projectile = df_projectile[df_projectile["x"] >= 0]

fig, ax = plt.subplots(figsize=(10, 6))
ax.scatter(df_projectile.t, df_projectile.x, label="Observed Displacement", color="C0")
ax.plot(df_projectile.t, df_projectile.x_true, label='True Function', color="C1")
ax.set(xlabel="Time (s)", ylabel="Displacement (m)", ylim=(0, None))
ax.legend();

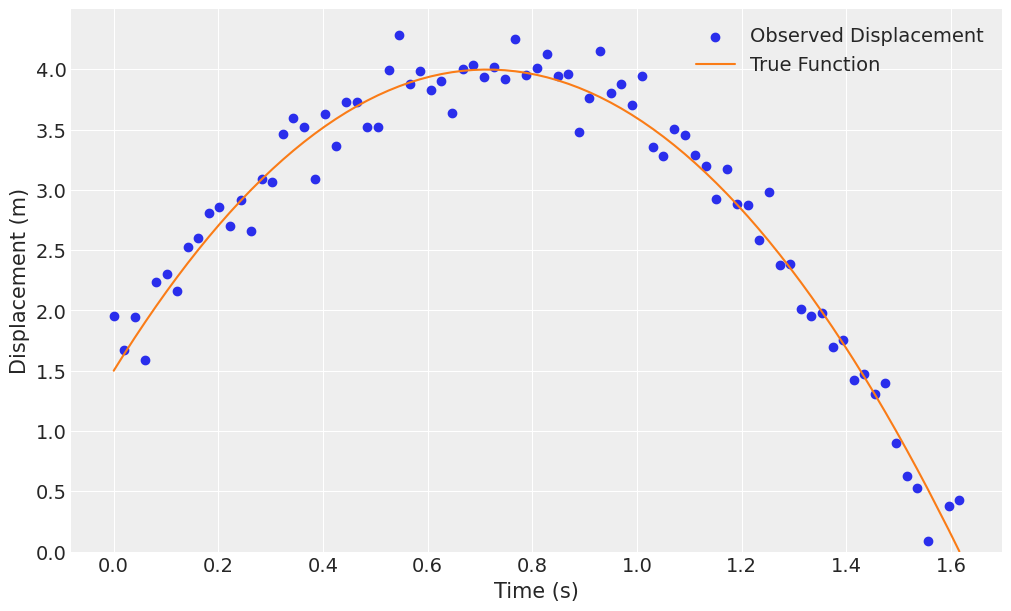
Projectile motion data

Modeling this using Bambi, we must include the linear term on time to capture the initial velocity. We’ll do the following regression,

\[x_f = \beta_0 + \beta_1 t + \beta_2 t^2\]

which then maps the solved coefficients to the following: \(\beta_0 = x_0\), \(\beta_1 = v_0\), and \(\beta_2 = \frac{g}{2}\).

model_projectile_all_terms = bmb.Model("x ~ I(t**2) + t + 1", df_projectile)
fit_projectile_all_terms = model_projectile_all_terms.fit(
    idata_kwargs={"log_likelihood": True}, target_accept=0.9, random_seed=SEED
)

az.summary(fit_projectile_all_terms)

            mean     sd  hdi_3%  hdi_97%  mcse_mean  mcse_sd  ess_bulk  ess_tail  r_hat
sigma      0.202  0.017   0.171    0.234      0.000    0.000    2723.0    2328.0    1.0
Intercept  1.561  0.066   1.441    1.687      0.001    0.001    2058.0    2550.0    1.0
I(t ** 2) -4.867  0.114  -5.079   -4.649      0.003    0.002    1667.0    1966.0    1.0
t          6.909  0.189   6.553    7.262      0.005    0.003    1694.0    2039.0    1.0

hdi = az.hdi(fit_projectile_all_terms.posterior, hdi_prob=0.95)
print(f"Initial height: {hdi['Intercept'].sel(hdi='lower'):.2f} to "
      f"{hdi['Intercept'].sel(hdi='higher'):.2f} meters (True: {x0} m)")
print(f"Initial velocity: {hdi['t'].sel(hdi='lower'):.2f} to "
      f"{hdi['t'].sel(hdi='higher'):.2f} meters per second (True: {v0} m/s)")
print(f"Acceleration: {2*hdi['I(t ** 2)'].sel(hdi='lower'):.2f} to "
      f"{2*hdi['I(t ** 2)'].sel(hdi='higher'):.2f} meters per second squared (True: {g} m/s^2)")

Initial height: 1.43 to 1.69 meters (True: 1.5 m)
Initial velocity: 6.54 to 7.28 meters per second (True: 7 m/s)
Acceleration: -10.16 to -9.27 meters per second squared (True: -9.81 m/s^2)

We once again are able to recover all our input parameters.

In addition to directly calculating all terms, to include all polynomial terms up to a given degree you can use the poly keyword. We don’t do that in this notebook for two reasons. First, by default it orthogonalizes the terms making it ill-suited to this example since the coefficients have physical meaning (more information on this in an upcoming post). The orthogonalization process can be disabled by the raw argument of poly, but we still elect not to use poly here because in later examples we decide to use different effects on the \(t\) term vs the \(t^2\) term, and doing so is not easy when using poly. However, just to show that the results match when using the raw = True argument, we’ll fit the same model as above.

model_poly_raw = bmb.Model("x ~ poly(t, 2, raw=True)", df_projectile)
fit_poly_raw = model_poly_raw.fit(idata_kwargs={"log_likelihood": True}, random_seed=SEED)
az.summary(fit_poly_raw)

                          mean     sd  hdi_3%  hdi_97%  mcse_mean  mcse_sd  ess_bulk  ess_tail  r_hat
sigma                    0.201  0.017   0.172    0.234      0.000    0.000    3066.0    2205.0    1.0
Intercept                1.561  0.067   1.437    1.682      0.001    0.001    2535.0    2154.0    1.0
poly(t, 2, raw=True)[0]  6.911  0.196   6.556    7.280      0.004    0.004    2092.0    2075.0    1.0
poly(t, 2, raw=True)[1] -4.870  0.118  -5.095   -4.653      0.003    0.002    2059.0    2166.0    1.0

We see the same results, where poly(t, 2, raw=True)[0] corresponds to the coefficient on \(t\) (\(v_0\) in our example), and poly(t, 2, raw=True)[1] is the coefficient on \(t^2\) (\(\frac{g}{2}\)).

Measuring gravity on a new planet

In the next example, you’ve been recruited to join the space program as a research scientist, looking to directly measure the gravity on a new planet, PlanetX. You don’t know anything about this planet or its safety, so you have time for one, and only one, throw of a ball. However, you’ve perfected your throwing mechanics, and can achieve the same initial velocity wherever you are. To baseline, you make a toss on planet Earth, warm up your spacecraft and stop at Mars to make a toss, then travel far away, and make a toss on PlanetX.

First we simulate data for this experiment.

def simulate_throw(v0, g, noise_std, time_step=0.25, max_time=10, seed=1234):
    rng = np.random.default_rng(seed)
    times = np.arange(0, max_time, time_step)
    heights = v0 * times - 0.5 * g * times**2
    heights_with_noise = heights + rng.normal(0, noise_std, len(times))
    valid_indices = heights_with_noise >= 0
    return times[valid_indices], heights_with_noise[valid_indices], heights[valid_indices]

# Define the parameters
v0 = 20  # Initial velocity (m/s)
g_planets = {"Earth": 9.81, "Mars": 3.72, "PlanetX": 6.0}
noise_std = 1.5

# Generate data
records = []
for planet, g in g_planets.items():
    times, heights, heights_true = simulate_throw(v0, g, noise_std)
    for time, height, height_true in zip(times, heights, heights_true):
        records.append([planet, time, height, height_true])

df = pd.DataFrame(records, columns=["Planet", "Time", "Height", "Height_true"])
df["Planet"] = df["Planet"].astype("category")

And drawing those trajectories,

fig, ax = plt.subplots(figsize=(10, 6))

for i, planet in enumerate(df["Planet"].cat.categories):
    subset = df[df["Planet"] == planet]
    ax.plot(subset["Time"], subset["Height_true"], alpha=0.7, color=f"C{i}")
    ax.scatter(subset["Time"], subset["Height"], alpha=0.7, label=planet, color=f"C{i}")

ax.set(
    xlabel="Time (seconds)", ylabel="Height (meters)",
    title="Trajectory Comparison", ylim=(0, None)
)
ax.legend(title="Planet");

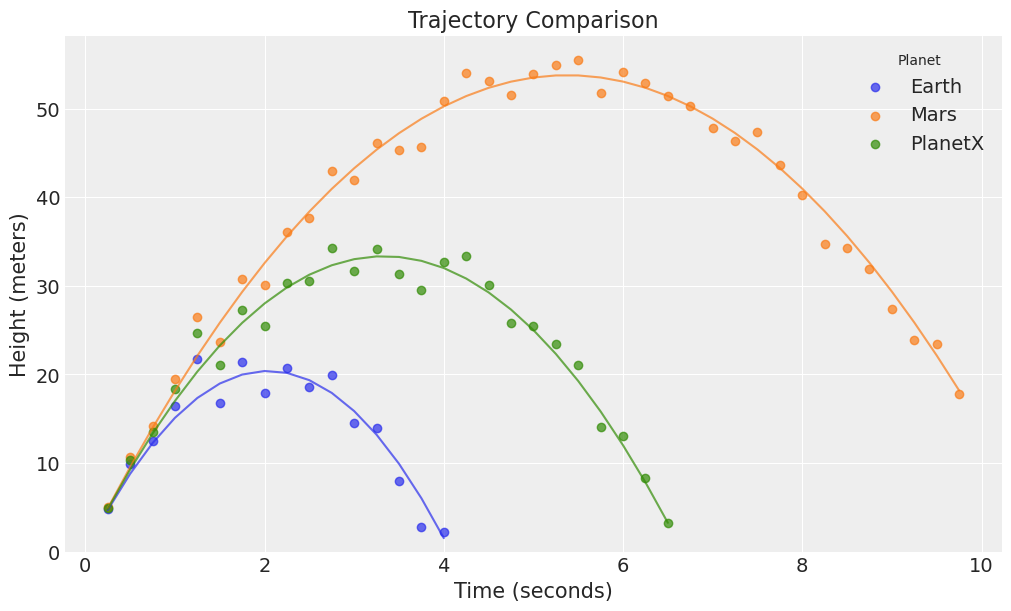
Planet trajectories

We now aim to model this data. We again use the following equation (calling displacement \(h\) for height):

\[h = \frac{1}{2} g_{p} t^2 + v_{0} t\]

where \(g_p\) now has a subscript to indicate the planet that we’re throwing from.

In Bambi, we’ll do the following:

Height ~ I(Time**2):Planet + Time + 0

which corresponds one-to-one with the above formula. The intercept is eliminated since we start from \(x=0\).

planet_model = bmb.Model("Height ~ I(Time**2):Planet + Time + 0", df)
planet_model.build()
planet_fit = planet_model.fit(chains=4, idata_kwargs={"log_likelihood": True}, random_seed=SEED)

The model has fit. Let’s look at how we did recovering the simulated parameters.

az.summary(planet_fit)

                                mean     sd  hdi_3%  hdi_97%  mcse_mean  mcse_sd  ess_bulk  ess_tail  r_hat
sigma                          1.759  0.147   1.498    2.044      0.003    0.003    2054.0    1938.0    1.0
I(Time ** 2):Planet[Earth]    -4.998  0.075  -5.145   -4.865      0.002    0.001    1833.0    2431.0    1.0
I(Time ** 2):Planet[Mars]     -1.884  0.022  -1.925   -1.844      0.001    0.000    1428.0    1763.0    1.0
I(Time ** 2):Planet[PlanetX]  -3.017  0.036  -3.087   -2.953      0.001    0.001    1519.0    1729.0    1.0
Time                          20.128  0.166  19.827   20.449      0.004    0.003    1393.0    1714.0    1.0

Getting the gravities back to the physical value,

hdi = az.hdi(planet_fit.posterior, hdi_prob=0.95)
print(f"g for Earth: {2*hdi['I(Time ** 2):Planet'].sel({'I(Time ** 2):Planet_dim':'Earth', 'hdi':'lower'}):.2f} "
      f"to {2*hdi['I(Time ** 2):Planet'].sel({'I(Time ** 2):Planet_dim':'Earth', 'hdi':'higher'}):.2f} "
      f"meters (True: -9.81 m)")
print(f"g for Mars: {2*hdi['I(Time ** 2):Planet'].sel({'I(Time ** 2):Planet_dim':'Mars', 'hdi':'lower'}):.2f} "
      f"to {2*hdi['I(Time ** 2):Planet'].sel({'I(Time ** 2):Planet_dim':'Mars', 'hdi':'higher'}):.2f} "
      f"meters (True: -3.72 m)")
print(f"g for PlanetX: {2*hdi['I(Time ** 2):Planet'].sel({'I(Time ** 2):Planet_dim':'PlanetX', 'hdi':'lower'}):.2f} "
      f"to {2*hdi['I(Time ** 2):Planet'].sel({'I(Time ** 2):Planet_dim':'PlanetX', 'hdi':'higher'}):.2f} "
      f"meters (True: -6.0 m)")
print(f"Initial velocity: {hdi['Time'].sel(hdi='lower'):.2f} to {hdi['Time'].sel(hdi='higher'):.2f} "
      f"meters per second (True: 20 m/s)")

g for Earth: -10.29 to -9.71 meters (True: -9.81 m)
g for Mars: -3.85 to -3.68 meters (True: -3.72 m)
g for PlanetX: -6.18 to -5.90 meters (True: -6.0 m)
Initial velocity: 19.80 to 20.45 meters per second (True: 20 m/s)

We can see that we’re pretty close to recovering most the parameters, but the fit isn’t great. Plotting the posteriors for \(g\) against the true values,

earth_posterior = -2 * planet_fit.posterior["I(Time ** 2):Planet"].sel(
    {"I(Time ** 2):Planet_dim": "Earth"})
planetx_posterior = -2 * planet_fit.posterior["I(Time ** 2):Planet"].sel(
    {"I(Time ** 2):Planet_dim": "PlanetX"})
mars_posterior = -2 * planet_fit.posterior["I(Time ** 2):Planet"].sel(
    {"I(Time ** 2):Planet_dim": "Mars"})

fig, axs = plt.subplots(1, 3, figsize=(12, 6))
az.plot_posterior(earth_posterior, ref_val=9.81, ax=axs[0])
axs[0].set_title("Posterior $g$ on Earth")
az.plot_posterior(mars_posterior, ref_val=3.72, ax=axs[1])
axs[1].set_title("Posterior $g$ on Mars")
az.plot_posterior(planetx_posterior, ref_val=6.0, ax=axs[2])
axs[2].set_title("Posterior $g$ on PlanetX");

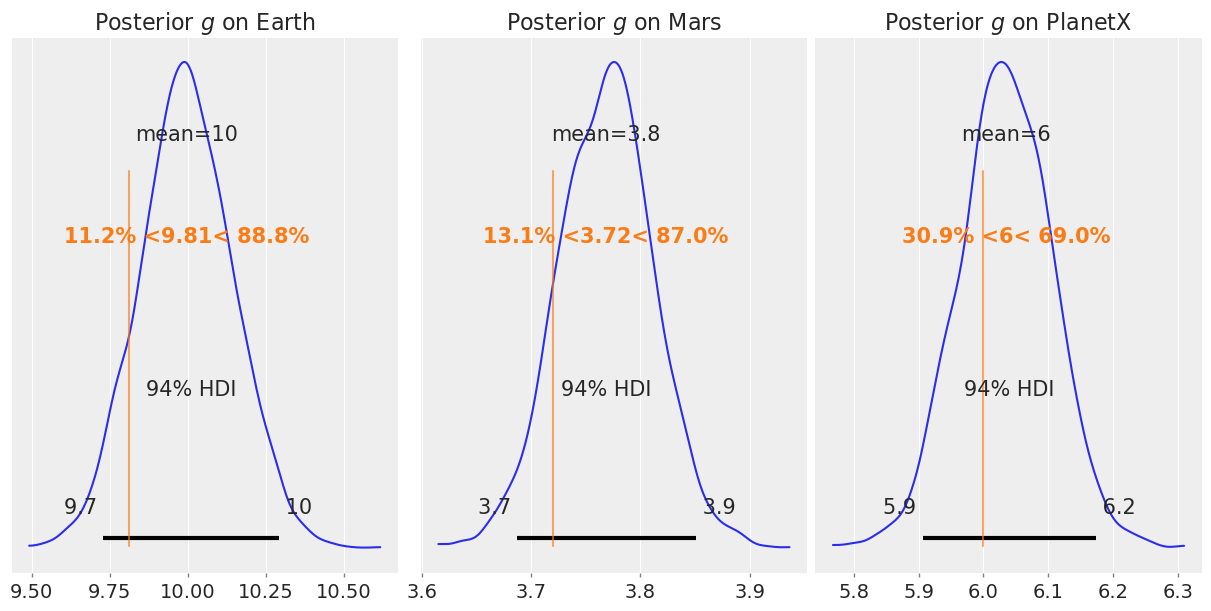
Gravity posteriors without prior

The fit seems to work, more or less, but certainly could be improved.

Adding a prior

But, we can do better! We have a very good idea of the acceleration due to gravity on Earth and Mars, so why not use that information? From an experimental standpoint, we can consider these throws from a calibration mindset, allowing us to get some information on the resolution of our detector, and our throwing apparatus. With informative priors constraining the Earth and Mars gravity parameters, the model can more precisely estimate the unknown PlanetX gravity, as there will be less uncertainty propagating from the calibration planets.

For Earth, at the extremes, \(g\) takes values as low as 9.78 \(m\)/\(s^2\) (at the Equator) up to 9.83 (at the Poles). So we can add a very strong prior,

\[g_{\text{Earth}} \sim \text{Normal}(-9.81, 0.025)\]

For Mars, we know the mean value is about 3.72 \(m\)/\(s^2\). There’s less information on local variation readily available by a cursory search, however we know that the radius of Mars is about half that of Earth, so \(\sigma = \frac{0.025}{2} = 0.0125\) might make sense, but to be conservative we’ll round that up to \(\sigma = 0.02\).

\[g_{\text{Mars}} \sim \text{Normal}(-3.72, 0.02)\]

For PlanetX, we must use a very loose prior. We might say that we know the ball took longer to fall than Earth, but not as long as on Mars, so we can split the difference. Then set a very wide \(\sigma\) value.

\[g_{\text{PlanetX}} \sim \text{Normal}(\frac{-9.81 - 3.72}{2}, 3) = \text{Normal}(-6.77, 3)\]

Since these correspond to \(g/2\), we’ll divide all values by 2 when putting them into Bambi. Additionally, we know the balls landed eventually, so \(g\) must be negative. We’ll truncate the upper limit of the distribution at 0.

Now, for defining this in Bambi, the term of interest is I(Time ** 2):Planet. Often, you set one prior that applies to all groups, however, if you want to set each group individually, you can pass a list to the bmb.Prior definition. The broadcasting rules from PyMC apply here, so it could equivalently take a numpy array. You’ll notice that the priors are passed alphabetically by group name.

priors = {
    "I(Time ** 2):Planet": bmb.Prior(
        "TruncatedNormal",
        mu=[
            -9.81/2,  # Earth
            -3.72/2,  # Mars
            -6.77/2   # PlanetX
        ],
        sigma=[
            0.025/2,  # Earth
            0.02/2,   # Mars
            3/2       # PlanetX
        ],
        upper=[0, 0, 0]
    )}

planet_model_with_prior = bmb.Model(
    'Height ~ I(Time**2):Planet + Time + 0',
    df,
    priors=priors
)

planet_model_with_prior.build()
idata = planet_model_with_prior.prior_predictive()
az.summary(idata.prior, kind="stats")

                                 mean       sd   hdi_3%  hdi_97%
sigma                          14.466   13.809    0.025   36.595
I(Time ** 2):Planet[Earth]     -4.905    0.012   -4.928   -4.883
I(Time ** 2):Planet[Mars]      -1.860    0.010   -1.880   -1.841
I(Time ** 2):Planet[PlanetX]   -3.622    1.509   -6.360   -0.915
Time                            0.520   14.788  -26.565   27.992

Here we’ve sampled the prior predictive and can see that our priors are correctly specified to the associated planets.

Next we fit the model.

planet_fit_with_prior = planet_model_with_prior.fit(
    chains=4, idata_kwargs={"log_likelihood": True}, random_seed=SEED
)
planet_model_with_prior.predict(planet_fit_with_prior, kind="pps");

az.summary(planet_fit_with_prior)[0:5]

                                mean     sd  hdi_3%  hdi_97%  mcse_mean  mcse_sd  ess_bulk  ess_tail  r_hat
sigma                          1.759  0.142   1.495    2.024      0.002    0.002    3333.0    2373.0    1.0
I(Time ** 2):Planet[Earth]    -4.907  0.012  -4.929   -4.884      0.000    0.000    4360.0    2943.0    1.0
I(Time ** 2):Planet[Mars]     -1.862  0.009  -1.879   -1.847      0.000    0.000    2054.0    2614.0    1.0
I(Time ** 2):Planet[PlanetX]  -2.985  0.023  -3.025   -2.940      0.000    0.000    2282.0    2772.0    1.0
Time                          19.960  0.075  19.827   20.103      0.002    0.001    2025.0    2249.0    1.0

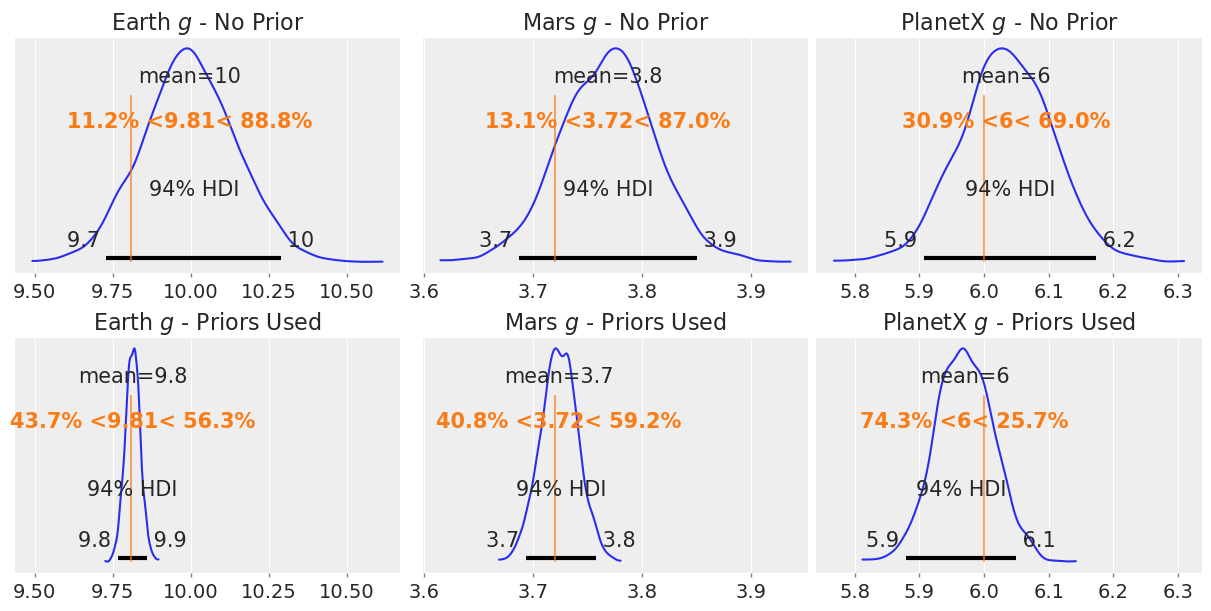
We see some improvements here! Off the cuff, these look better, you’ll notice the \(v_0\) coefficient on Time covers the true value of 20 m/s.

Now taking a look at the effects before and after adding the prior on the gravities,

earth_posterior_2 = -2 * planet_fit_with_prior.posterior["I(Time ** 2):Planet"].sel(
    {"I(Time ** 2):Planet_dim": "Earth"})
mars_posterior_2 = -2 * planet_fit_with_prior.posterior["I(Time ** 2):Planet"].sel(
    {"I(Time ** 2):Planet_dim": "Mars"})
planetx_posterior_2 = -2 * planet_fit_with_prior.posterior["I(Time ** 2):Planet"].sel(
    {"I(Time ** 2):Planet_dim": "PlanetX"})

fig, axs = plt.subplots(2, 3, figsize=(12, 6), sharex='col')
az.plot_posterior(earth_posterior, ref_val=9.81, ax=axs[0,0])
axs[0,0].set_title("Earth $g$ - No Prior")
az.plot_posterior(mars_posterior, ref_val=3.72, ax=axs[0,1])
axs[0,1].set_title("Mars $g$ - No Prior")
az.plot_posterior(planetx_posterior, ref_val=6.0, ax=axs[0,2])
axs[0,2].set_title("PlanetX $g$ - No Prior")

az.plot_posterior(earth_posterior_2, ref_val=9.81, ax=axs[1,0])
axs[1,0].set_title("Earth $g$ - Priors Used")
az.plot_posterior(mars_posterior_2, ref_val=3.72, ax=axs[1,1])
axs[1,1].set_title("Mars $g$ - Priors Used")
az.plot_posterior(planetx_posterior_2, ref_val=6.0, ax=axs[1,2])
axs[1,2].set_title("PlanetX $g$ - Priors Used");

Gravity posteriors comparison

Adding the prior gives smaller uncertainties for Earth and Mars by design, however, we can see the estimate for PlanetX has also improved by injecting our knowledge into the model.

2026 2
2025 1
2023 2
2022 3
2021 2
2020 13
2019 10
2018 4
2017 1

2026