2023 Reading List
Books I read in 2023
This week’s Riddler Express was one I managed to solve analytically, but I’ve also included some plots in R for some post-problem analysis, just for fun.
From Dan Levin comes a hazardous riddle for the ironclad and eagle-eyed:
The U.S. Open concluded last weekend, with physics major Bryson DeChambeau emerging victorious. Seeing his favorite golfer win his first major got Dan thinking about the precision needed to be a professional at the sport.
A typical hole is about 400 yards long, while the cup measures a mere 4.25 inches in diameter. Suppose that, with every swing, you hit the ball X percent closer to the center of the hole. For example, if X were 75 percent, then with every swing the ball would be four times closer to the hole than it was previously.
For a 400-yard hole, assuming there are no hazards (water, sand or otherwise) in the way, what is the minimum value of X so that you’ll shoot par, meaning you’ll hit the ball into the cup in exactly four strokes?
Let the initial distance from the tee to the hole be \(d_0\). The percent of the total distance covered by each shot is given by \(x\). Then, the remaining distance to the hole after the first hit is given by
\begin{equation} d_1 = d_0 (1-x) \end{equation}
Similarly, the distance after the second hit is given by
\begin{equation}
d_2 = d_1(1-x)
d_2 = (d_0(1-x))(1-x) = d_0(1-x)^2
\end{equation}
It follows that after $N$ strokes, the remaining distance is given by
\begin{equation} d_N = d_0(1-x)^N \end{equation}
To estimate when the hit would land in the hole, we want \(d_N=r\), the hole’s radius. At this point, the center of the ball will lie on the edge of the hole and we can assume gravity will do the trick. If we want that to achieve a par of 4, then this must occur when \(N=4\). The problem gives a course length of \(d_0=14,400\) (400 yards in inches), and \(r=4.25/2=2.125\).
\begin{equation}
d_4 = d_0(1-x)^4
2.125 = 14400(1-x)^4
x \approx 0.89
\end{equation}
Just to get a more visual understanding of the problem, I’m including some additional plots.
First, looking at percentage of distance covered as a function of shots for a “par-level” player (covering 89% of the distance per shot),
x <- 0:6
y<-lapply(x, {function (i) (1-0.89)^i})
plot(x, y, col="firebrick",
xlab="Shot Number",
ylab="Percent of Total Distance Remaining" )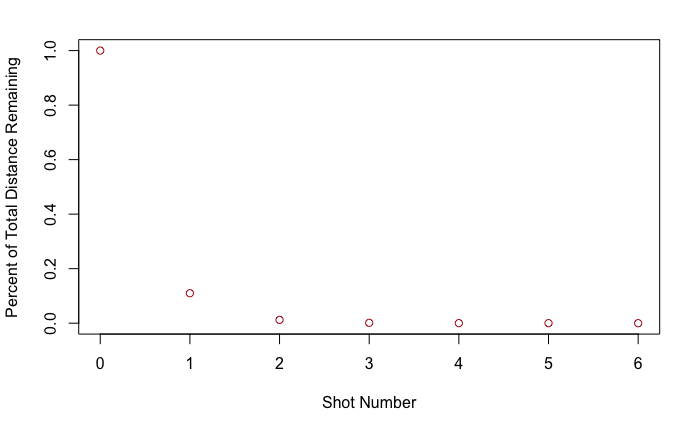
Next, the number of strokes to make it in a hole at 400 yards for various distance percentage values. Solving for N gives,
\begin{equation}
\frac{14400}{2.125} = (1-x)^N
N = \frac{\ln(14400/2.125)}{\ln(1-x)}
\end{equation}
Of course, N is constrained to \(\Bbb Z^+\) (positive integers), so a ceiling round is applied.
x <- seq(0.05,0.95,0.05)
y <- lapply(x, {function (x) (ceiling(log(2.125/14400)/log(1-x))) })
plot(x, y, col="firebrick",
xlab="Percent Distance Covered per Shot",
ylab="Shots Needed to Reach Hole" )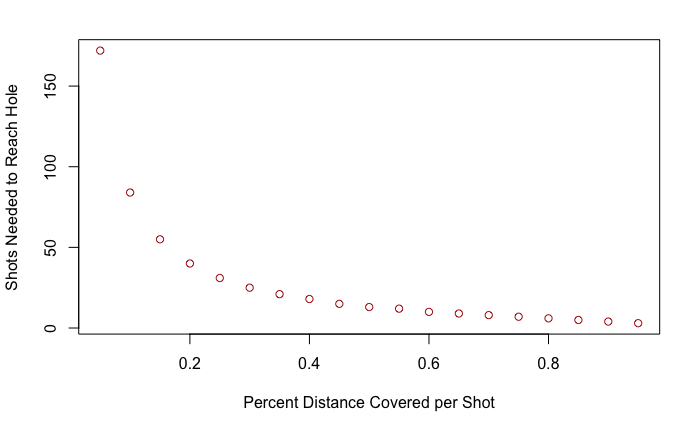
Books I read in 2023
Who will win this year’s cup?
Books I read in 2022
Just how lucky have the 18-3 Bruins gotten?
Interoperability is the name of the game
Books I read in 2021
I got a job!
Books I read in 2020
Revisiting some old work, and handling some heteroscadasticity
Using a Bayesian GLM in order to see if a lack of fans translates to a lack of home-field advantage
An analytical solution plus some plots in R (yes, you read that right, R)
okay… I made a small mistake
Creating a practical application for the hit classifier (along with some reflections on the model development)
Diving into resampling to sort out a very imbalanced class problem
Or, ‘how I learned the word pneumonoultramicroscopicsilicovolcanoconiosis’
Amping up the hit outcome model with feature engineering and hyperparameter optimization
Can we classify the outcome of a baseball hit based on the hit kinematics?
Updates on my PhD dissertation progress and defense
My bread baking adventures and favorite recipes
A summary of my experience applying to work in MLB Front Offices over the 2019-2020 offseason
Books I read in 2019
Busting out the trusty random number generator
Perhaps we’re being a bit hyperbolic
Revisiting more fake-baseball for 538
A deep-dive into Lance Lynn’s recent dominance
Fresh-off-the-press Higgs results!
How do theoretical players stack up against Joe Dimaggio?
I went to Pittsburgh to talk Higgs
If baseball isn’t random enough, let’s make it into a dice game
Random one-off visualizations from 2019
Books I read in 2018
Or: how to summarize a PhD’s worth of work in 8 minutes
Double the Higgs, double the fun!
A data-driven summary of the 2018 Reddit /r/Baseball Trade Deadline Game
A 2017 player analysis of Tommy Pham