Fivethirtyeight Riddler: Which Baseball Team Will Win The Riddler Fall Classic?

This weekend I took on fivethirtyeight’s weekly Riddler question again. The original problem text can be found here.

Riddler Express

Problem statement:

If a baseball team is truly .500, meaning it has a 50 percent chance of winning each game, what’s the probability that it has won two of its last four games and four of its last eight games?

Solution:

The solution to this was pretty straightforward. Basically my approach was to run a coin flip simulation 8 times, since those odds are 50/50, equivalent to a .500 team. I did this in python using a random boolean, where 1 was “heads” and 0 was “tails.” I first look at the subset of the first 4 of those, and if 2/4 are are “heads,” then I look at the full set of 8. If 4/8 are “heads,” then I consider this “passing.”

I run this simulation over and over, and find the ratio of passing to the total number of attempts, shown in this plot (note the log scaled x-axis):

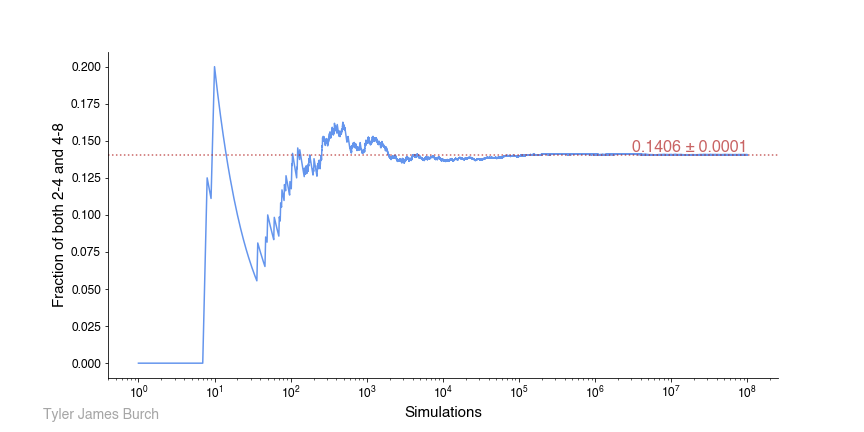
Since the simulation wasn’t very intensive, 100,000,000 attempts were made, converging on a probability of 0.1406 ± 0.0001. For the uncertainty, I took the 95% confidence interval, as calculated using the Agresti–Coull interval, where the CI is z*sqrt(p*(1-p)/N), for p “passing results,” N attempts, and z value of 1.96 corresponding to the 95% CI.

The full Jupyter notebook for this solution can be found here.

Riddler Classic

Problem statement:

Riddler League Baseball, also known as the RLB, consists of three teams: the Mississippi Moonwalkers, the Delaware Doubloons and the Tennessee Taters.

Each time a batter for the Moonwalkers comes to the plate, they have a 40 percent chance of getting a walk and a 60 percent chance of striking out. Each batter for the Doubloons, meanwhile, hits a double 20 percent percent of the time, driving in any teammates who are on base, and strikes out the remaining 80 percent of the time. Finally, each batter for the Taters has a 10 percent chance of hitting a home run and a 90 percent chance of striking out.

During the RLB season, each team plays an equal number of games against each opponent. Games are nine innings long and can go into extra innings just like in other baseball leagues. Which of the three teams is most likely to have the best record at the end of the season?

Solution:

The solution to this took a bit more involved simulation. What I did was reprise my simulation for the baseball yahtzee puzzle earlier this year, gut it out a little bit and adapt it to this specific problem, with the given actions and likelihoods.

The Jupyter notebook found here shows the complete game definition in the various classes as the top, and the simulation indicated. This simulation was a lot more intensive, I ended up doing each matchup 500,000 times for a total of 1,500,000 games.

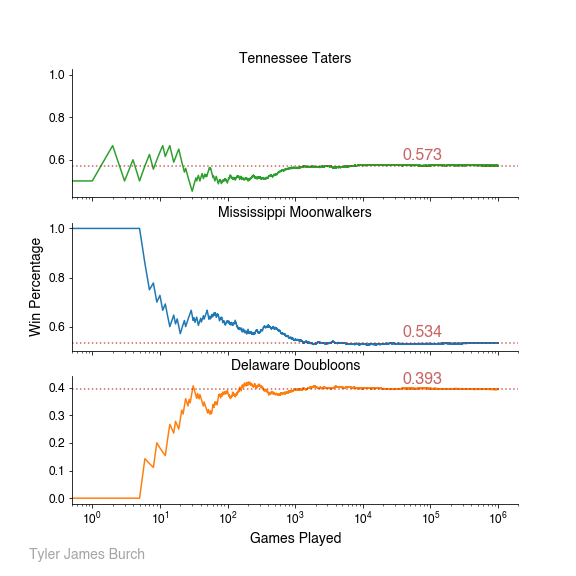
The solution found that:

The Tennessee Taters have the best record at a .573 winning percentage.

The Mississippi Moonwalkers were in the middle with a .534 winning percentage.

The Delaware Doubloons were the worst with a .393 winning percentage.

I also plotted winning percentage as games were played, to see how the solution evolved as games were simulated:

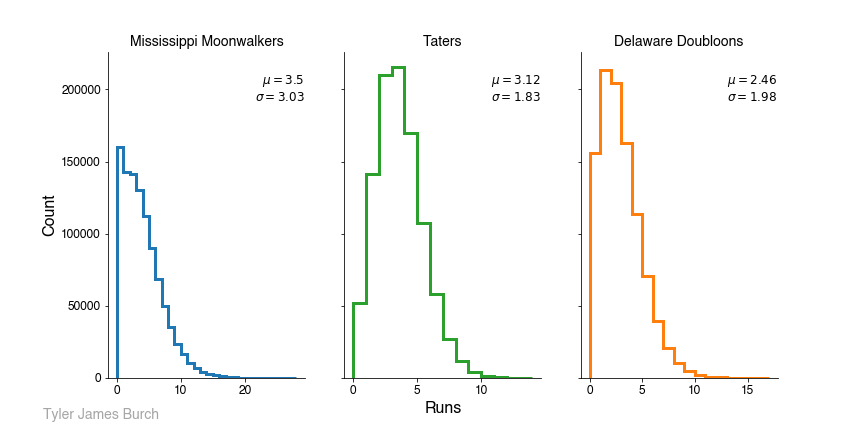
Also of interest was the scoring distribution of each team, to better understand the game as defined. Since we know the actions and rates of each team, it’s interesting to see exactly how those translate to runs within the confines of a standard baseball game.

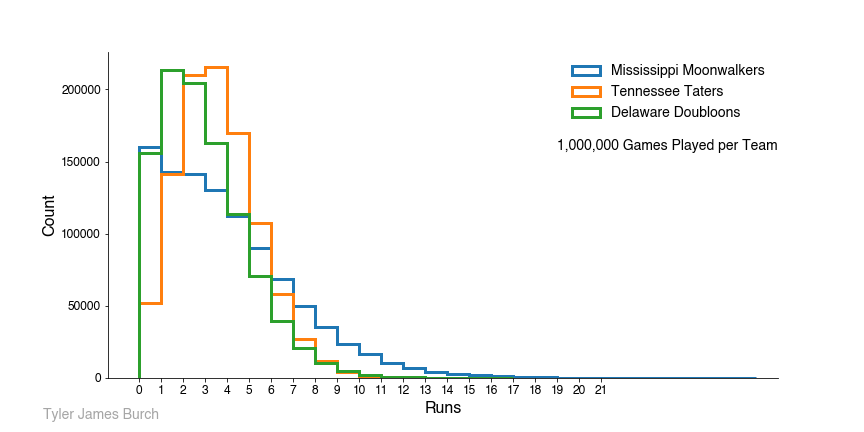
We can also overlay these onto one plot:

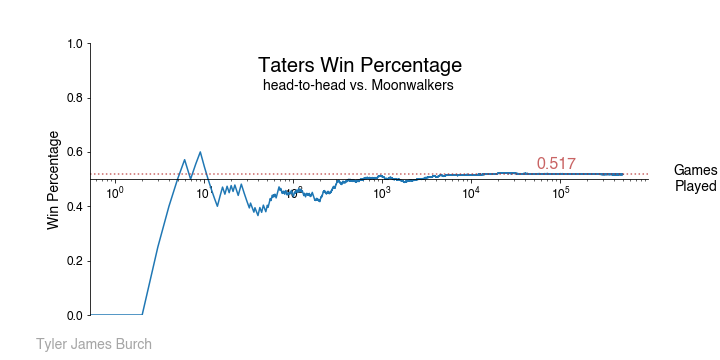
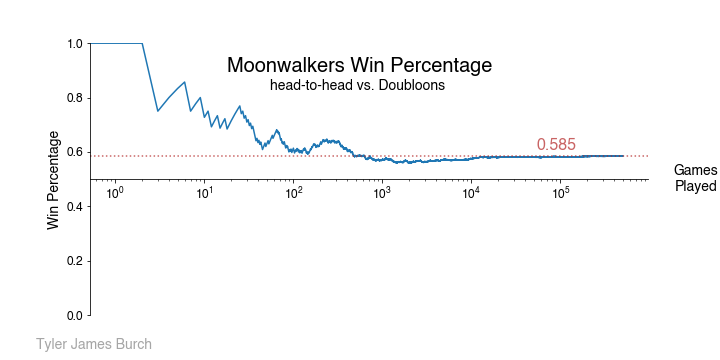
Last, we can look at head-to-head winning percentages. These plots were made from the winning team’s perspective, but to get the losing team’s winning percentage, you’d just mirror over the x-axis.

• 2023 1
• 2022 2
• 2021 1
• 2020 10
• 2019 8
• 2018 3
• 2017 1